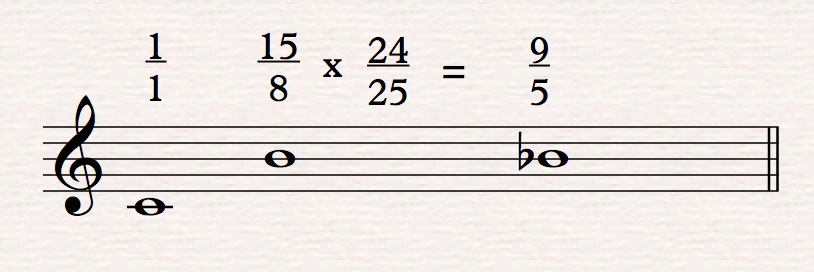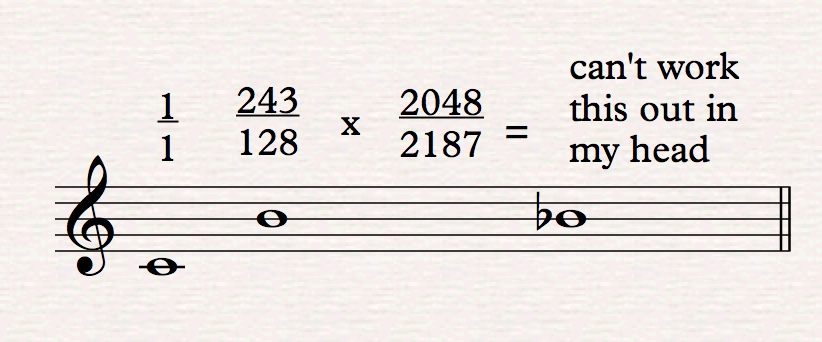How to Use Ben Johnston's
Just Intonation NotationI have worked with Ben Johnston's just-intonation pitch notation since 1983, and find it intuitive and elegant; I compose in it, in my head. It is, of course, not the only microtonal pitch notation available. Its great advantage over others is that the scores of Johnston's amazing body of music are written in it, as well as the musics of Toby Twining (including his astounding Chrysalid Requiem) and Adam Silverman, along with my own music, as well as the transcriptions I've seen of Harry Partch's music. Such a repertoire justifies some familiarity with this notation. Other notations have other advantages, and thinking in them will possibly lead to different composing tendencies, but notation is only a means to an end, and I feel that ultimately a notation can only be justified by the music written in it. I hope the outline of rules given here will expand understanding of this notation for those interested in it and in this music.
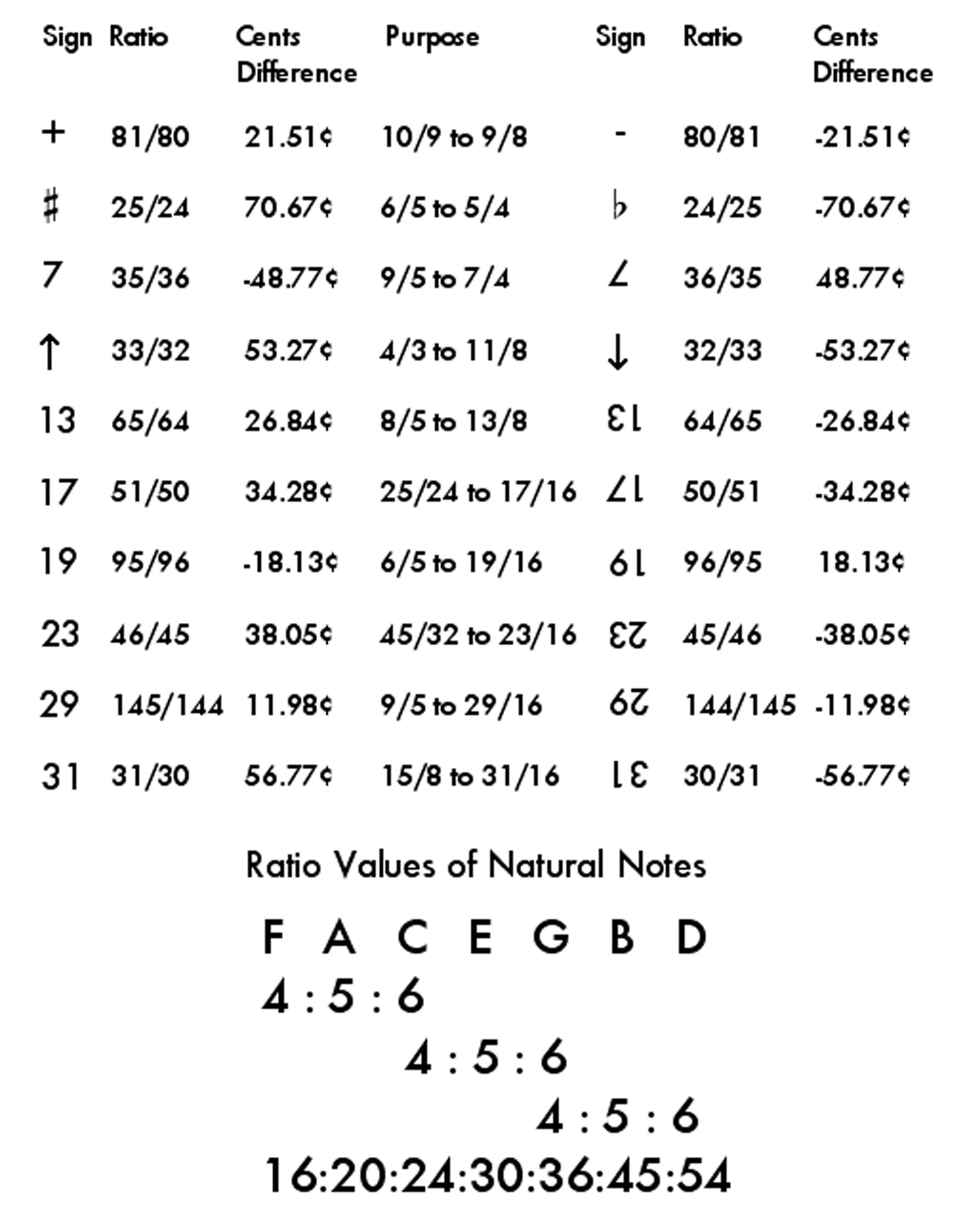
It was recognized in the 16th century that an accidental placed in front of a note multiplies that pitch's frequency by a conventional constant; for instance, a sharp (#) multiplies a pitch by 25/24, raising a minor third (6/5) to a major third (5/4). Johnston's notation for just intonation is based on and extends this principle, that every accidental multiplies a pitch's frequency by some defined constant. Running up to the 31st harmonic or down to the 31st subharmonic, the examples he devised are shown in this chart:
These accidentals can be combined to create pitches with sometimes very elaborate names:
By convention the plus or minus is kept separate, and to the right of the other accidentals. Means of combining accidentals have not yet been entirely standardized.
It is assumed in this notation that F-A-C, C-E-G, and G-B-D are perfectly tuned major triads of 4:5:6. Because of this, certain other triads, such as D-F-A and Bb-D-F, are not well tuned without modification. If you look at a cycle of perfect five-limit thirds in Johnston's notation:
you will see that for intervals above D in this cycle, pluses must be added to keep the intervals simple, and below F minuses must be added. Pluses and minuses represent the syntonic comma, 81/80. Another (sometimes easier) way to keep this in mind is that the all-natural scale is identical to Ptolemy's tense diatonic scale as defined around 1900 years ago (called by Partch the "Ptolemaic sequence"), the simplest form of the just-tuned major scale:
As you can see, C, F, and A have major seconds of 9/8 automatically built on them, but on D and G you need a major second with a plus to arrive at 9/8. And since 16/15 x 25/24 (sharped) = 10/9, E and B need pluses added to the major second to be 9/8 as well (E F#+, B C#+).
In this notational system it's important to keep in mind that while F-C-G-D and A-E-B are all perfect fifths of 3/2, D up to A is not 3/2, but 40/27 (the ratio of 9/8 to 5/3). Likewise F to Bb isn't 4/3, but 27/20, since F to B is 45/32 (F-G being 9/8 and G-B being 5/4; 9/8 x 5/4 = 45/32). 45/32 x 24/25 (Bb) = 27/20. The correct 4/3 above F needs a minus: Bb-. For triads and seventh chords the cycle of thirds above gives the simple five-limit tunings. Still, these pluses and minuses are in a sense bookkeeping, and the more important concepts concern the other accidentals.
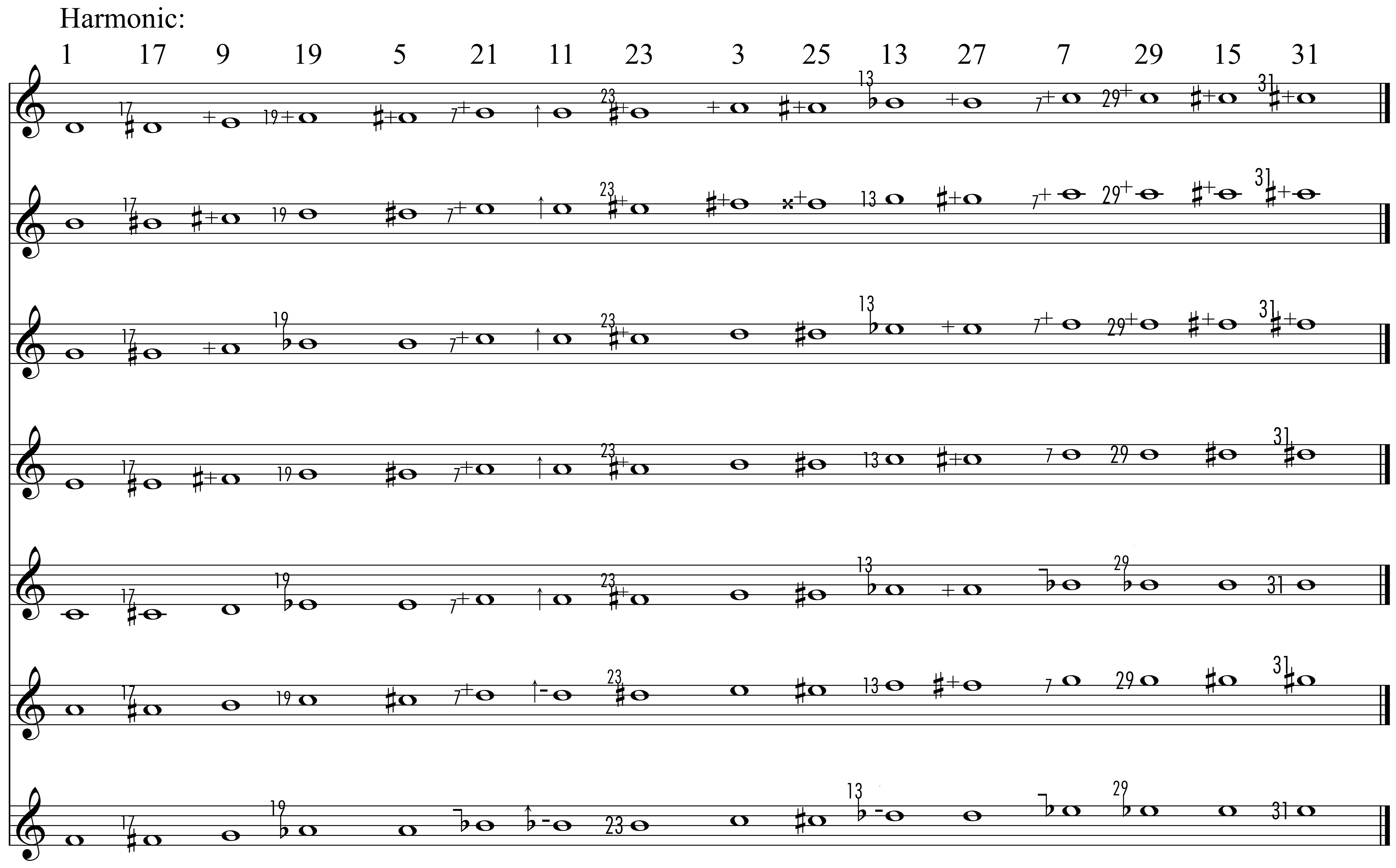
This chart, which I made decades ago, helped me initially in learning the relationships between accidentals. It consists of the first 31 harmonics of all seven natural notes. By transposing the intervals via accidentals added equally to each note, a myriad new intervals can be drawn and understood:
For instance, in the 5 and 11 columns we have two notes making an 11/10 interval at seven different transposition levels. By adding the same accidental(s) to both notes in any of those pairs, we can transpose that interval virtually anywhere.
No two non-identical pitches, no matter how close, can ever have the same notation; no two pitches differently notated can ever be the same pitch. Despite the foregoing complications, which are not difficult to master, I have found this a wonderfully exact and intuitive notation for composing. (Performing it on instruments is sometimes a different matter, depending on the music's complexity.)
Deriving Ratios from the Notation
To derive a ratio from the notation of two pitches involves starting with the basic interval between natural notes and multiplying by the added accidentals. It might be helpful here to encapsulate all the ratios among the seven natural notes:

I'll give three examples:
In the first one, F to A13bv (A-thirteen-flat-down-arrow), F to A is 5/4; the 13 will multiply this basic interval by by 65/64, the flat by 24/25, and the down-arrow by 32/33. 5/4 x 65/64 x 24/25 x 32/33 = 13/11 (it takes some factoring out to reach the answer in simplest terms; I have many notebooks filled with such calculations. The 25 in the denominator cancels out the 5 in the numerators and also the factor 5 within 65, leaving 13. The 24 above and the 33 below work out to 8/11, and so on.) One step can be subtracted if you can remember that F to Ab is 6/5, thus you can start from 6/5 instead of 5/4 and omit the 24/25.
If there is an accidental on the lower note, the interval should be multiplied by the inversion of that accidental's value, since an accidental lowering the lower note will increase the interval's size, and vice versa. For instance, for C+ to Eb^, we start with C to E being 5/4; we multiply by 24/25 for the flat, by 33/32 for the up-arrow, but for the plus we have to multiply by 80/81 (rather than 81/80), because being on the lower note it narrows the interval by raising the pitch. 5/4 x 24/25 x 33/32 x 80/81 = 11/9.
In Ab to D-upside-down-13, you might tend to assume that A to D is 4/3, but it isn't. A to D- is 4/3. A to D, calculated from the numbers on the top chart above, is 27/20. The upside-down 13 multiplies by 64/65, and the flat on A, which increases the interval size, multiplies by 25/24. 27/20 [the original A to D interval] x 64/65 [the upside-down 13] x 25/24 [the lower flat] = 18/13.
Deriving the Notation from Ratios
It may seem more difficult, at first, to start with a desired ratio and imagine what its pitch expression would be, but this too is a rule-based process. Keep in mind that when we multiply a pitch by 7 we are moving to its seventh harmonic, which is an octave of a minor seventh; when we divide a frequency by 11, we move to its 11th subharmonic, which is some octave of a fourth below. Also, each accidental is intended to modify a specific interval; for instance, the up-arrow changes a 4/3 interval to an 11/8, and since 4/3 is a perfect fourth, for an 11/8 we always start with a perfect fourth and add an up-arrow. Likewise, the 13 (65/64) changes an 8/5 to a 13/8, and since 8/5 is a minor sixth, we always start with a minor sixth and add the 13. An important principle is: if there is an 11 in the numerator there must be an up-arrow in the accidental (unless the note the interval is based on contains a down-arrow, which would cancel it out). If there is a 13 in the denominator, there must be an upside-down 13 in the accidental (unless the interval is based on a pitch containing a right-side-up 13.) And so on, for each prime factor larger than 5.
The complete and consistent set of rules for deriving a pitch name from a ratio, up through the 19-limit, is as follows:
Sort the ratio into its prime factors. We can disregard 2 and all powers of 2 as octaves, signifiers of register rather than pitch name. For our purposes, 12/11 is effectively 3/11.
There are no enharmonic equivalents in this notation. If the direction is to move by a minor sixth, an augmented fifth (though the same on the goddamn piano) will give the wrong answer.
For every 3 in the numerator:
Ascend one perfect fifth. (Add a plus to the perfect fifth note if starting on any kind of B or D, including Bb, D#, B-, whatever. If the original note had a minus, the plus will merely cancel it out on the new note.)For every 5 in the numerator:
Ascend one major 3rd. (Add plus if starting on a D.)For every 7 in the numerator:
Ascend one minor seventh and add a 7. (Add plus if starting on a G, B, or D.)For every 9 in the numerator:
Ascend one major second. (Add plus if starting on an E, G, B, or D.)For every 11 in the numerator:
Ascend one perfect fourth and add ^ (up-arrow). (Add minus if starting on an A or F.)For every 13 in the numerator:
Ascend one minor sixth and add a 13. (Add minus if starting on an F.)For every 17 in the numerator:
Add a sharp and a 17.For every 19 in the numerator:
Ascend a minor third and add a 19. (Add plus if starting on a D.)For every 3 in the denominator:
Descend one perfect fifth. (Add minus if starting on an A or F.)For every 5 in the denominator:
Descend one major 3rd. (Add minus if starting on an F.)For every 7 in the denominator:
Descend one minor seventh and add a L (sub-7). (Add minus if starting on an F, A, or C.)For every 9 in the denominator:
Descend one major second. (Add minus if starting on an F, A, C, or E.)For every 11 in the denominator:
Descend one perfect fourth and add v (down-arrow). (Add plus if starting on a B or D.)For every 13 in the denominator:
Descend one minor sixth and add an upside-down 13. (Add plus if starting on a D.)For every 17 in the denominator:
Add a flat and an upside-down 17.For every 19 in the denominator:
Descend a minor third and add an upside-down 19. (Add minus if starting on an F.)Here are four examples. For the ratio 21/13 we need a 3 and a 7 going up, and a 13 coming down:
For the ratio 44/25 we need an 11 going up (we can ignore the 4 as denoting two octaves), and two 5s coming down:
For the ratio 64/49 we can ignore the 64 as being a power of 2 (octaves) and we need two 7s coming down:
Building a ratio from a note with accidentals sometimes involves canceling out those accidentals when their inverses are called for, as in this 77/60 based on E-sharp-down-arrow-sub-seven as 1/1:
Follow these rules, and within a week or two of practice it will become fairly easy to convert ratios into musical notation. Remembering where one needs a plus or minus is the difficult part, and even I, after 35 years, have to sometimes check myself afterward by multiplying ratios to make sure I reached the correct solution; but even that generally becomes second nature. For most musical purposes, the notation will clarify the harmonic relationships, and you'll be able to tell whether the notes look correct together in context.
For fonts for Ben Johnston's notation, see Andrian Pertout's web site.
ADDENDUM: I am sometimes asked why I don't switch to HEWM notation instead of Johnston, as they are closely related. HEWM (Helmholtz-Ellis-Wolf-Monzo) notation starts with the Pythagorean scale instead of the Ptolemaic sequence, so that pluses and minuses never apply to perfect fifths, and are always correlated to five-based ratios. It offers more mathematical consistency in that respect.
Here's one of my reasons. Say I'm in the key of C and want a B-flat. In Johnston's notation, if C is 1/1, B is 15/8. To get B-flat I multiply by 24/25, the value of a flat:
In HEWM notation, the B is 243/128, and the flat I multiply by has a value of 2048/2187:
A calculator tells me it's 16/9. I've always regarded consistency as one of the less important virtues, and if I'm going to compose with ratios, constantly computing them in my head, I don't want to have a lot of four-digit numbers to multiply and divide. Others may have different criteria. Also, as a microtonalist friend who doesn't use Johnston notation remarked to me recently, Ben's notation "is so intuitive that I can always figure out what's going on," which isn't true of some of the alternatives. Of course, the primary and sufficient justification for Johnston's notation is that great music has been written in it. Any notation in which great music has been written is worthy of study.
From Johnston's String Quartet No. 9:
If you find any problems with the examples, e-mail me here.